Research

Randomized iterative methods for large linear systems
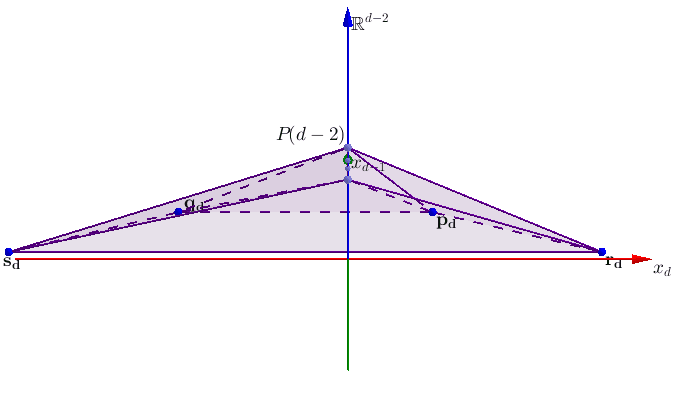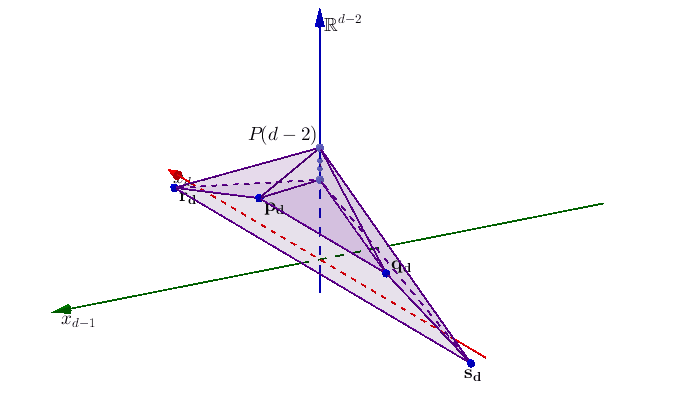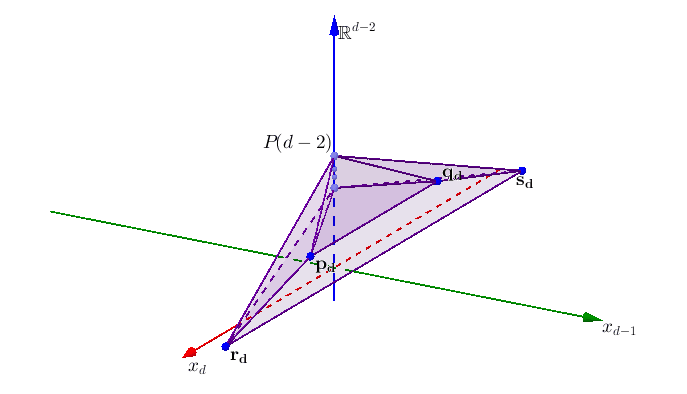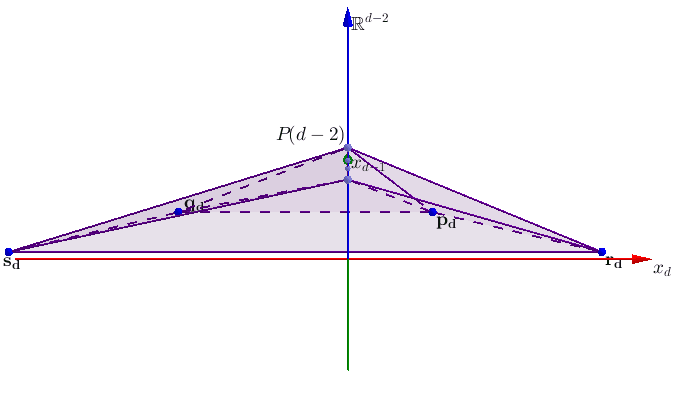
Solving large systems of linear equations and inequalities efficiently and effectively is one of the most common and foundational problems encountered in the data-rich sciences. One pillar of my research is developing iterative projection techniques for solving systems of such large scale that the problem-defining data cannot be held entirely in computer memory. My research has analyzed Kaczmarz methods for a variety of problems, such as systems of linear inequalities, graph-defined systems, or noisy and corrupted systems of equations.[ Publications ] [ Slides ] [ Video ]
Combinatorial methods for constrained convex optimization
Many iterative methods for convex optimization are numerical and convergent in nature, however, for select problems, there are common combinatorial (finite) methods. Wolfe's method is a finite algorithm for computing the projection onto a convex polytope, and its complexity was unknown since the introduction of the method in the 1970s; with collaborators, I showed that this method has exponential behavior in the worst case. Recently, I have been considering the Hanson-Lawson method for nonnegative least-squares.[ Publications ] [ Slides ]
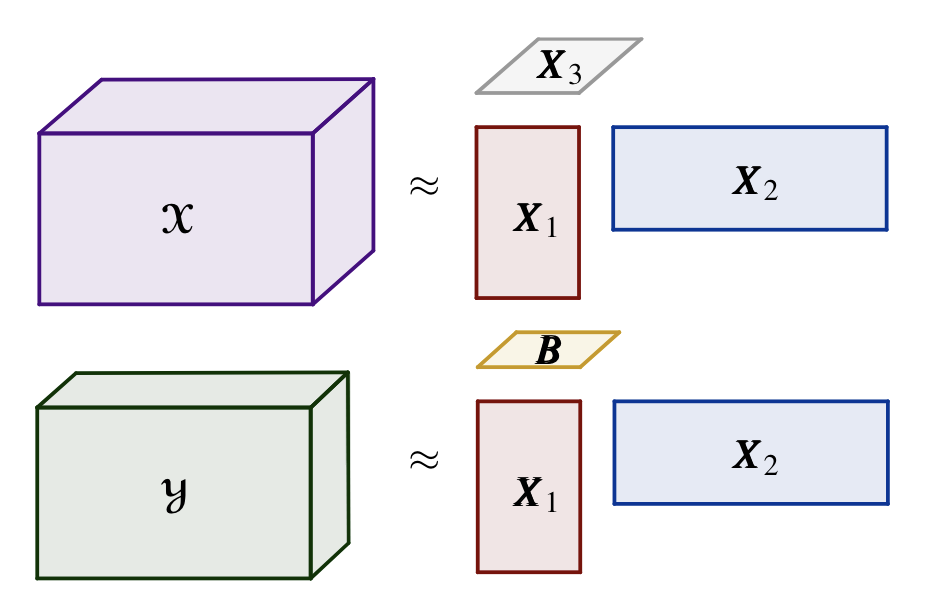
Matrix factorization and tensor decomposition for topic modeling
There is currently an unprecedented demand for interpretable methods to study large-scale, multi-modal tensor data. and represented well by a tensor. My research develops matrix factorization and tensor decomposition models for learning the latent topics in the data while respecting the natural multi-modal structure of the data, and which allow for incorporation of flexible supervision information, and identify hierarchical topic structure, and to design and analyze efficient methods for training these models.[ Publications ] [ Slides ] [ Video ]
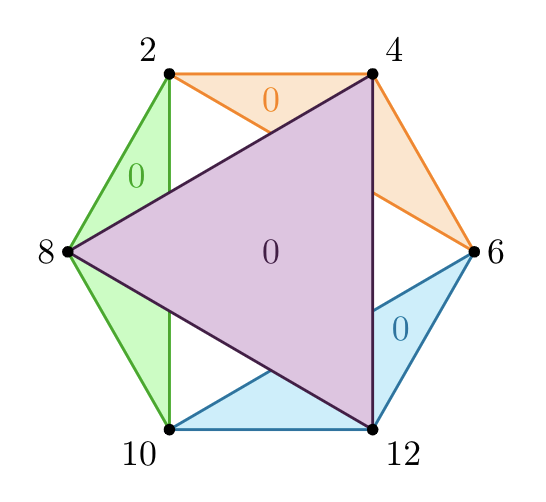
Network consensus and ranking
Consensus and ranking problems can be understood as learning values for each node of a graph which respect some pairwise measurements (defining the edges of the graph). One can utilize tools from numerical linear algebra, combinatorial linear algebra, and the analysis of iterative techniques for linear systems to design and analyze methods for solving these problems. In particular, my research has focused on gossip methods for the average consensus problem, and recently has developed these types of methods for the ranking problem.[ Publications ] [ Slides ]
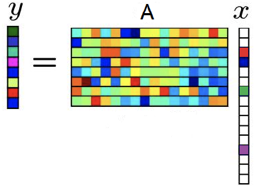
Methods in compressive sensing
Compressive sensing techniques have revolutionized sensing and sampling, with applications in image reconstruction, hyper spectral imaging, wireless communications, and analog to digital conversion. Meanwhile, complex data-gathering devices have been developed, leading to problem instances so large that they cannot be stored or solved in conventional computers. My research has developed and analyzed asynchronous parallel sparse recovery methods for such problem, as well as learning models for selecting classical CS methods.[ Publications ]
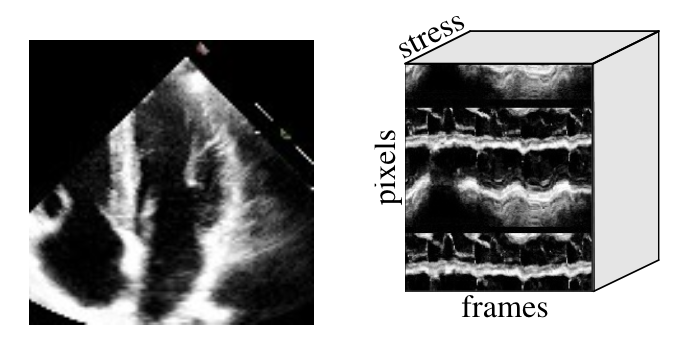
Data science applications in medicine
I have been fortunate to be part of wonderful collaborations applying data scientific, mathematical, and statistical approaches to medically relevant data from various application partners. With Homeboy Industries, we performed thorough statistical tests analyzing data regarding side effects from tattoo removal. With LymeDisease.org, we performed various analyses on large-scale survey data from Lyme patients. My grant NSF DMS #2211318 currently funds a collaboration with the UCLA-Harbor Medical Center Department of Cardiology.[ Publications ]
Community detection on graphs and hypergraphs
Detecting latent community structure amonst entities with pairwise (or group-wise) relationships, e.g., graphs and hypergraphs, is a fundamental and widely-applicable task. With my collaborators, I have been investigating efficient spectral methods for detecting communities in various stochastic graph and hypergraph models, and thresholds for detectability using these techniques. I additionally consider provable matrix and tensor decomposition techniques for this task.[ Publications ] [ Slides ]
Eigenvalue problems in combinatorial linear algebra and zero-forcing
Combinatorial linear algebra and combinatorial inverse problems find application in many areas, including in engineering design. My research has considered combinatorial inverse problems, including understanding the minimum number of eigenvalues of certain graph-structured matrices. This problem is related to zero-forcing, a dynamic graph process in which nodes of a specific color force the color change of their neighbors. We have also considered a probabilistic zero-forcing measure on graphs.[ Publications ]
Note: The lovely gif at the top of the page is due to my exceptional student Hannah Kaufman! This is a visualization of the Kaczmarz method.
